3月20日，一个研究团队发表论文称，他们找到了一种神奇的十三边形，可以无缝隙且无规律地拼出一个无限的平面图案，他们将这种形状的图形命名为“帽子”。

　　这个图形被认为就是世界各地的数学家们都在寻找的能“无周期平铺”的首个“爱因斯坦瓦片”，又称“爱因斯坦单铺砌块”。

　　在铺砌领域，数学家们一直在追寻一种可以填满无限平面且不会有规律重复的“非周期性”铺砌块。它与著名物理学家爱因斯坦同名，都叫“爱因斯坦”，在德语中的ein Stein，即是“一块石头”的意思。

　　这种单铺砌块的“非周期性”，其实是指由这种形状构成的整体图案，“不能通过平移或旋转来恢复相同的图案”。它不同于像国际象棋棋盘那样的图案，那种棋盘图案如果平移两格，看上去也毫无区别。

　　人们发现，要寻找这种非周期性、非重复性铺砌的图案竟相当不容易。数学家们最初发现的非周期铺砌块是由超过两万种形状组成的，但后来才慢慢减少到仅由两种形状组成的非周期铺砌块，也就是著名的彭罗斯铺砌。

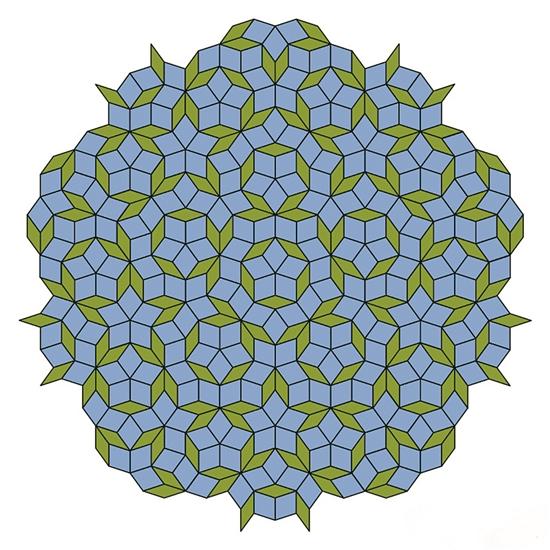
　　它是在20世纪70年代，由数学家罗杰·彭罗斯发现的，使用了两种不同的菱形完成了非周期性铺砌。这两个形状组成的图案在现代的很多家居装饰中常常会出现。彭罗斯平铺包含多种对称性，但它永远无法周期性重复。

　　数学家们一直在努力寻找只用一种图形就能完成这种非周期性铺砌的“爱因斯坦瓦片”。一开始，他们甚至都不确定这种图形是不是真的存在。

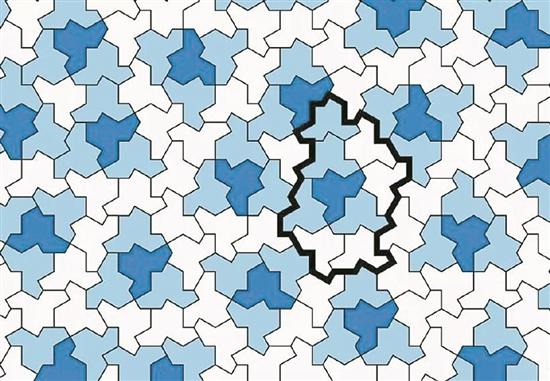
　　但终于，这个图形被英国东约克郡一位退休印刷技术员大卫·史密斯发现了——这是一个十三边形（也称为十三角形），它有一个特殊的性质：它可以被分成四个更小的相同形状（称为子瓦片），或者可以被组合成四个更大的相同形状（称为超级瓦片）。

　　这意味着这个十三边形可以无限地缩小或放大，并能用来铺满一个平面，而不会“周期性”地出现有规律重复的图案。

　　发现这个图形的史密斯给这个图形起了一个有趣的名字：帽子。因为它看起来像一顶礼帽。

　　史密斯并不是一个专业的数学家，但他曾经设计过一种叫做“史密斯拼图”的新型拼图。它由一些不规则的形状组成，可以拼成任何你想要的图案。

　　他还曾经发明过一种新型的骰子，叫做“史密斯骰子”，它也是由一些不同形状的多面体组成，可拿来玩各种游戏。

　　史密斯说，“爱因斯坦瓦片”的发现，灵感来自于一本关于无周期平铺的书籍，以及一些网上的资源。他用电脑软件来设计和测试形状，最后花了大约两年的时间才找到了这个十三边形，并证明了它是一个“爱因斯坦瓦片”。

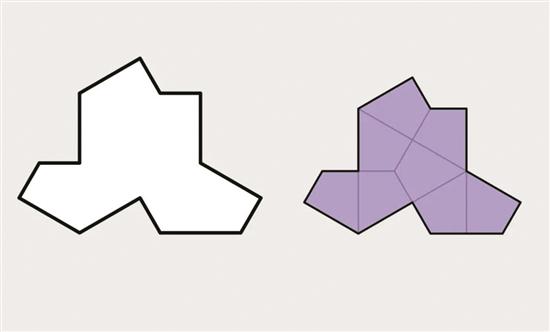
　　最后，史密斯和他的合作者们将这个发现发表在了数学专业杂志《几何与拓扑》上。他们还计划制作一些实体模型，以展示它们的形状在三维空间中是如何排列和变化的。

　　史密斯说，他希望他的发现能够激发更多人对数学和艺术之间的联系感兴趣，还可以为未来可能有用的应用打开新的可能性。

　　“我认为这是一个很有价值和有趣的领域，希望可以继续探索和创造更多有趣的图案。”他同时也认为，“帽子”也不可能会成为寻找“爱因斯坦”瓦片的终点。

　　例如2011年的诺贝尔化学奖，就授予了发现准晶体的材料科学家。准晶体是一种有着有序且永不重复的原子排列的材料，它们通常被描述为彭罗斯铺砌的类似物。由此可见，新发现的非周期性单铺砌块很有可能会带来材料科学的新进展。

　　此外，“帽子”也可以给艺术家们带来灵感。或许不久，我们就发现，这个图案已出现在各种潮牌的设计中。(更多新闻资讯，请关注羊城派